It is important to be efficient, not only in everyday life, but in computer science as well. Being efficient means that you 'achieve maximum productivity' using as few resources as possible. For computers, we want to try to solve problems by implementing algorithms which use as few resources (such as memory) as possible. How can this be accomplished? It is done by analyzing the implementations of computer programs, and determining whether or not a problem can be solved in a simpler, more efficient manner.

In this course, our focus on the efficiency of algorithms relates mostly to the implementation (the code itself).
We often use the notion of Big-O to describe the runtime of an alogrithm. Big-O is described loosely as an upper bound on the runtime of an algorithm. Here is an example of Big-O notation:
def thing(L):
count = 0
for i in range(len(L)):
if L[i] == 1:
for j in range(len(L)):
count += 1
return count
from time import time, clock
L = [1]*1000 #length of list here is 1000
start = time()
thing(L)
print("Time elapsed for thing: {} for {} items".format(time() - start, len(L)))
Since there are two for loops in this function, we expect this function to be O(n^2). What does this mean, though? Well when I run this program with different lengths for the input L, I receive these outputs:
Time elapsed for thing: 0.14109086990356445 for 1000 items
Time elapsed for thing: 1.0326859951019287 for 3000 items
Time elapsed for thing: 3.1200690269470215 for 5000 items
Since I said this algorithm was O(n^2), I expect that when I triple the size of the list L, the function should take 3^2 = 9 times as long to run. Similarly, when I multiply the size of the list L by 5, the function should take 5^2 = 25 times as long to run. The data above seem to support this theory.
However, this algorithm will not always have quadratic runtime. If the if statement fails every time the inner loop gets executed, the algorithm will have linear runtime. This is why Big-O is only an upper bound, it does not tell you that all inputs will have runtimes which grow in a quadratic manner.
Sorting Algorithms
In this course, we learned about some sorting algorithms which are better than the basic Bubble Sort, Insertion Sort, and Selection Sort. These are Quick Sort and Merge Sort. Quicksort works by choosing a 'pivot' and partitioning the entire list into 2 lists, where one contains all items greater than the pivot, and the other list contains all items which are less than the pivot. It then recursively sorts both lists. The base case is a list of length 1 which is already sorted.
In this course, we learned about some sorting algorithms which are better than the basic Bubble Sort, Insertion Sort, and Selection Sort. These are Quick Sort and Merge Sort. Quicksort works by choosing a 'pivot' and partitioning the entire list into 2 lists, where one contains all items greater than the pivot, and the other list contains all items which are less than the pivot. It then recursively sorts both lists. The base case is a list of length 1 which is already sorted.
Quick sort on average, is O(n log n). The log n part comes from the fact that we have to choose at least log n pivots to partition the list into 2 parts. The n factor comes from the fact that we have to compare each item in the entire list to the pivot, which requires about n comparisons.
Quick sort may have O(n^2) performance in its worst case. If the pivot chosen does not partition the list into 2 even sections every time, it is likely that more than log n (but no more than n) pivots will be chosen.
Merge sort always should have O(n log n) performance. It always operates the same way each time, by splitting the list into parts, until each part has only 1 element in it. Then, it re-merges all these parts together. The log n part comes from the fact that we make log n 'splits', and the n factor comes from the fact that we need to make n comparisons for the merging process.
Even though n log n < n^2 for large n, it is not certain that algorithms with O(n log n) performance will always outperform algorithms with O(n^2) performance. It is only more likely that they will for large n (inputs of large size). As seen below, when n is small (such as n < 10), algorithms which grow quadratically or even exponentially outperform the log n algorithm. But of course when n is very large, the log n algorithm 'wins'.
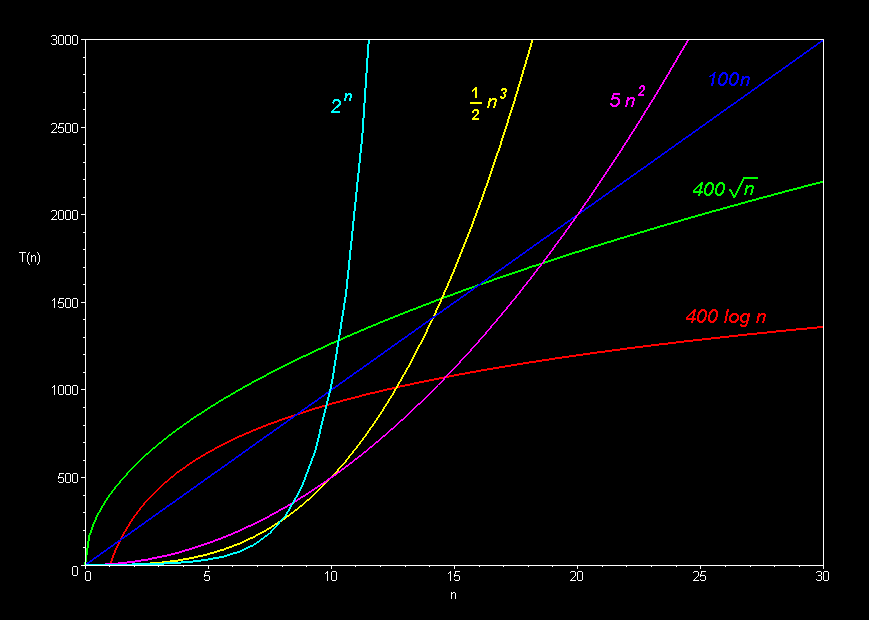
Another thing to consider is whether the elements in your list are close to being sorted or not. For example, if you choose your pivot in quick sort to be the first element in the list all the time, then in an almost sorted list, the algorithm will have to choose more than log n pivots, which will decrease the performance of quick sort.
So, it would make more sense to either use merge sort in this situation, or find a way to tweak quick sort so you don't run into this problem.
Conclusion:
Efficiency of algorithms should not be overlooked since it can be difference between a program running in 10 seconds vs. a program running in 10 minutes. Although we are concerned with how long a program takes to execute, we are more concerned with how an algorithm performs when the size of the input increases.

No comments:
Post a Comment